emoji-learn
What is emoji-learn? 🤔
emoji-learns is a simple library to create neural networks - in Emojicode!
How can this not be awesome??
Motivation 💪🏼

Look and Feel 👀
So…how does machine learning in Emojicode actually look like?? Here are some screenshots to save you an extra click to my GitHub repo:
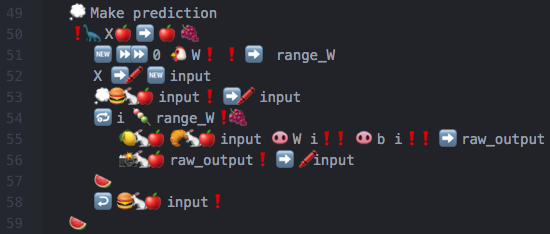
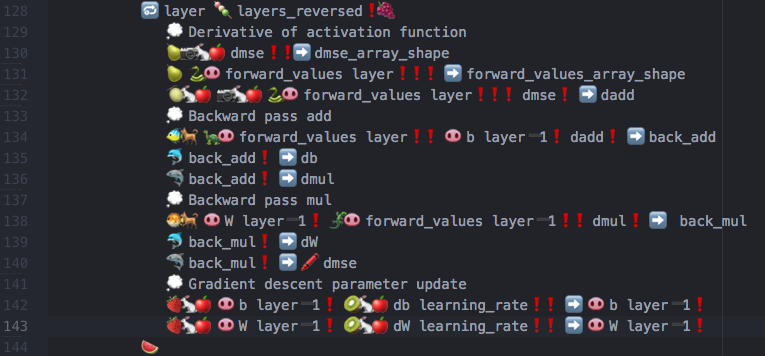
Yeah, it really is something.
Prerequisites 📝
Emojicode version 0.9+ is required. Go here to find out how to install it.
If you want to find out how to use Emojicode go through the excellent language reference or package index.
After you cloned the repository you at first have to build the numlol package. Go to packages/numlol and run the command
emojicodec -p numlol numlol.emojic
This will generate the numlol package.The emoji-learn package depends on this. So afterwards go to packages/emoji-learn and run
emojicodec -p emoji-learn -S /path/to/GitRepo/emoji-learn/packages emoji-learn.emojic
Documentation 🤓
numlol 💯
Machine learning and especially neural nets rely heavily on the use of linear algebra (LinAlg) - we need to add, subtract and multiply matrices and vectors. Unfortunately, the only data structure available in the standard Emojicode package that comes close to what we need are lists.
💭 A list of integers
🍨 1 2 3 4 5🍆
Because of this emoji-learn ships with a dedicated LinAlg-library called numlol (not to be confused with the imposters from numpy).
Creating a new numlol array is as simple as one-two-three, just hand over an embedded list to its constructor.
💭 Create a 3*2 matrix and store it in the variable 'matrix'
🆕🍎🆕 🍨🍨 1.0 2.0 🍆
🍨 3.0 4.0 🍆
🍨 5.0 6.0 🍆🍆 ❗➡️ matrix
💭 Create a 3*1 vector and store it in the variable 'vector'
🆕🍎🆕 🍨🍨 1.0 🍆
🍨 3.0 🍆
🍨 5.0 🍆🍆 ❗➡️ vector
In the numlol package all kind of matrix and vector operations are implemented: (Note: most methods are implemented as static methods so that the method name itself is followed by 🐇🍎)
Want to add two vectors? No problem!
💭 Elementwise addition of two arrays with the same shape
🍋🐇🍎 array01 array02❗➡️ sum_array
You suddenly need to transpose a matrix? Here you go!
💭 Transpose array
🍔🐇🍎 array❗➡️ transposed_array
It is necessary to perform a matrix-matrix/matrix-vector multiplication? Sure!
💭 Do matrix-matrix/matrix-vector multiplication
🥐🐇🍎 array01 array02❗➡️ multiplied_array
It also contains some more complicated functions we will need for machine learning later, e.g. the mean squared error function (👬) or the logistic activation function (📸).
It is also easy to print arrays to the console.
💭 Print array to console
📠 array❗
This will produce an output similar to the following

emoji-learn 📚
Ah, machine learning! The stuff all the cool kids do. So let’s dive right into it.
First of all we need data. A lot of it. At the moment the only way to get data in our net is via a .csv file. So your data should look like this
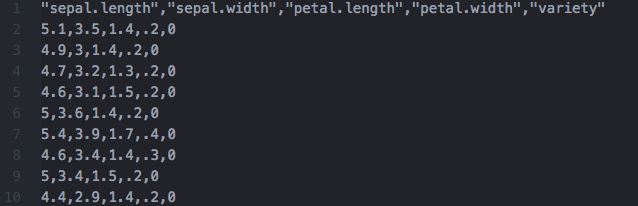
Then this file content can be transferred into a numlol array with just one method call
💭 Read .csv file into numlol array
🦋🐇🕸 🔤datasets/iris.csv🔤❗ ➡️ data
This method does not just read the data, but already normalizes the features and performs a one-hot encoding on the labels. You don’t have any datasets you can try out? No problem, we got you! There are already some toy datasets included.
💭 Read the iris dataset into a numlol array
🌺🐇🕸 ❗ ➡️ data
💭 Read the Pima Indians diabetes dataset into a numlol array
🛶🐇🕸 ❗ ➡️ data
💭 Read the sonar dataset into a numlol array
🚢🐇🕸 ❗ ➡️ data
Unfortunately an Emojicode method cannot return multiple values. Therefore ‘data’ is a value type that holds the features and the labels. There are two methods to access them both.
💭 Access features and labels from the 'data' value type
🐬 data❗ ➡️ X
🦈 data❗ ➡️ y
Next step is to split the data in a train and a test set. There is also a handy method for this.
💭 Split in train and test data
💭 0.333 means that (about) a third of all the data will be in the test data
🐅🐇🕸 X y 0.333❗ ➡️ train_test_data
Afterwards we can create our net. The constructor for the net expects just one parameter, a list with integers where each integer defines the number of neurons in each layer.
💭 Create a neural net. This one has:
💭 - 60 neurons in the input layer
💭 - 12 neurons in the hidden layer
💭 - 2 neurons in the output layer
💭 The number of hidden layers is NOT limited to one.
💭 It can be arbitrary (big)
🆕🕸🆕 🍨 60 12 2🍆 ❗➡️ neural_net
And now the magic takes place, we can train the net!
💭 Train the net with the given data over 100 epochs with a learning rate of 0.1
🦄 neural_net X_train y_train 100 0.1❗
To evaluate the performance we can finally calculate and print the accuracy.
💭 Train the net with the given data over 100 epochs with a learning rate of 0.1
🦍 neural_net X_test y_test❗ ➡️ accuracy_test
😀🍪 🔤Accuracy test data: 🔤 🔡accuracy_test✖️100 2❗🔤%🔤 🍪❗
This method can then be used to make predictions.
💭 Get the 3rd sample from the array X, make a prediction and print the result
📠 🦕 neural_net 🥫🐇🍎 X 3❗❗❗
Performance 📈
So, how does an Emojicode net performs on different datasets? I made a 10 fold crossvalidation training each net over 100 epochs, and here are the results (accuracies):
| X | Iris dataset | Sonar dataset | Pima Indian diabetes dataset |
|---|---|---|---|
| Train | 0.966 +/- 0.011 | 0.9986 +/- 0.0030 | 0.833 +/- 0.015 |
| Test | 0.980 +/- 0.023 | 0.784 +/- 0.029 | 0.746 +/- 0.026 |
Wow, not too bad!